以前、d-hacksの新人向け勉強会を実施した時に以下2つの質問をもらったのですが、その場であまりうまく答えられた自信がなく、改めて調べ直しも兼ねてまとめました。勉強のお役に立てば幸いです。

Q. 活性化関数はなぜ必要なのか？

深層学習におけるニューラルネットワークで活性化関数が重要なのは、複雑な関数を表現できるようにするため。基本的にはReLU関数が最もよく使われており、最近のLLMでは勾配消失を防ぐ目的でGeLU関数が使われている。
ReLU関数は単純で、$\mathrm{ReLU}(x)=\mathrm{max}(0,x)$ で表され、0以上の時だけ $y = x$ になる。

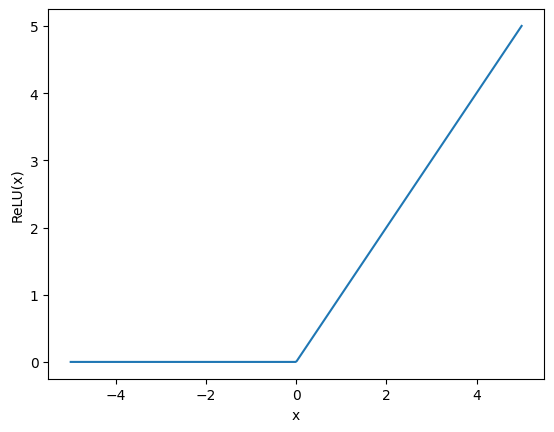
• 線形関数
  • （2次元のグラフにおいて）原点を通る直線のこと
  • 深層学習における線形層（Linear Layer）は、$y = wx + b$ のように原点を通らないアフィン変換の意もだいたい含む
• 非線形関数
  • ReLU、GeLU、Leaky ReLU、シグモイド、…

もし活性化関数を入れずに線形層だけを重ねると、何層重ねても全体としては1回の線形変換（アフィン変換）と同じになってしまう。
具体的に説明すると、ニューラルネットワークにおける各ノードは、入力 $x$ に対して重み $w$ を掛け、バイアス $b$ を加える変換を行う。
$y = wx + b$

一見すると、これを何層も重ねれば複雑な計算ができそうに見える。
$w_3 ( w_2 ( w_1 x + b_1 ) + b_2 ) + b_3$

が、この式はまとめると
$w' x + b'$
となり、結局は1回の線形変換（アフィン変換）と同じになってしまう。

2次元のグラフで考えると、活性化関数なしだと変換前も変換後も直線のままで、複雑な関数を近似することはできない。

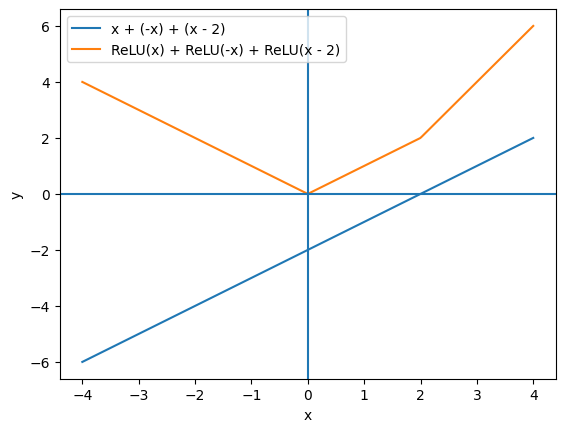
実際に2層でシグモイド関数を近似してみる

活性化関数を組み合わせた2次元グラフを見ることで、ニューラルネットワークにおける活性化関数の動作が分かりやすくなる。

ニューラルネットワークにおける1つのノードは、入力を重み $w_i$ 付きで足し合わせ、そこにバイアス $b_i$ を加え、最後に活性化関数を通す。
活性化関数をReLUとし、2層（隠れ層が1つ）の1入力1出力のニューラルネットワークは、次のように書ける。

$h_i = \mathrm{ReLU}( w_i^{(1)} x + b_i^{(1)})$
$y = \mathrm{ReLU}( w_0^{(2)} x + \sum_{i=1}^{m} w_i^{(2)} h_i + b^{(2)} )$

$\sum_{i=1}^{m} w_i^{(2)} h_i$ は、同じ層にある複数のノードの出力を足し合わせたもので、$h_i$ は隠れ層の出力のことを指す。

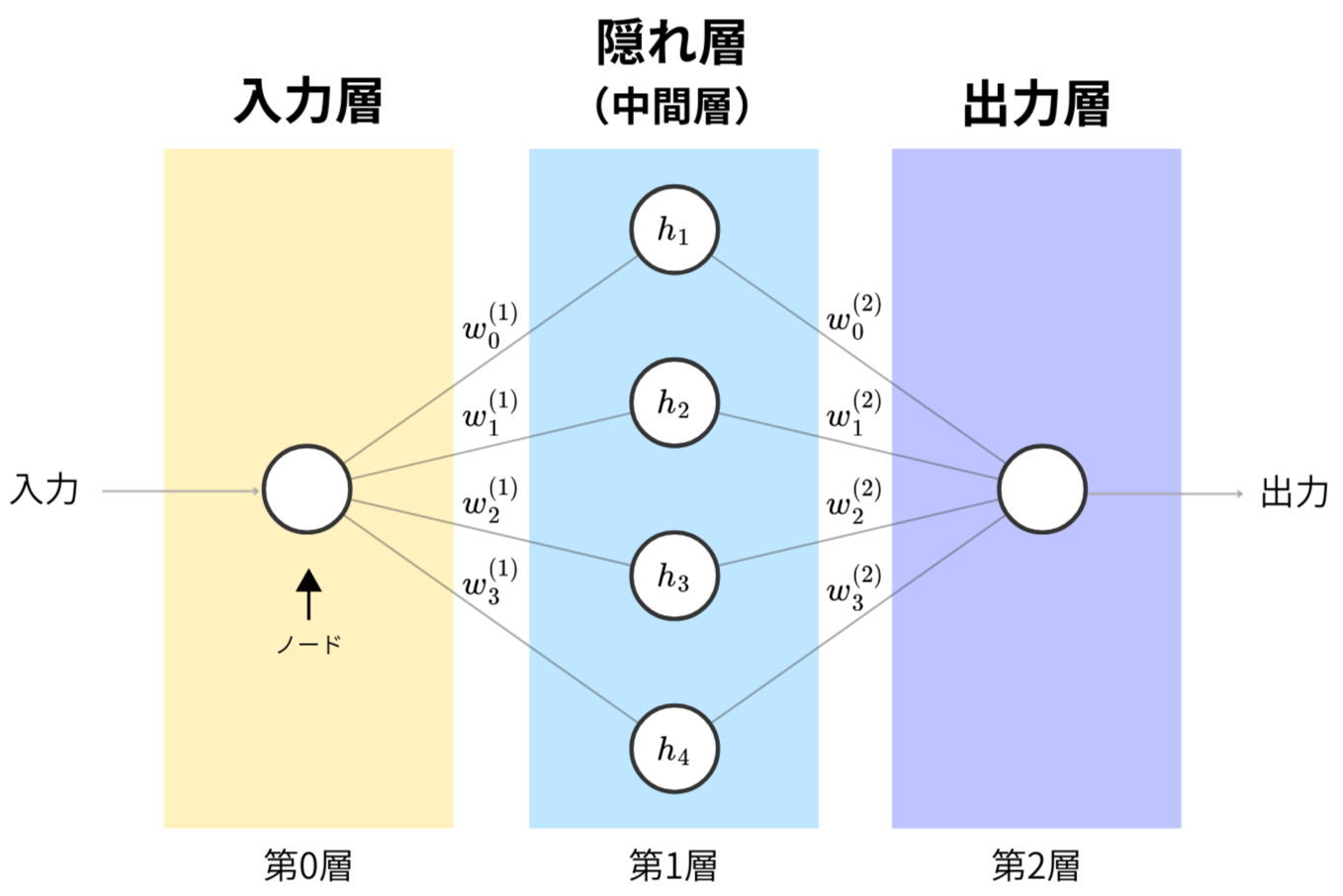
数式だけだとイメージしにくいと思うので、図で表すと分かりやすい。
隠れ層のノード数を4として、先ほどの式を用いて構成された2層ニューラルネットワークの図を以下に作った。それぞれの丸い部分はノードと呼ばれる。

これを使って、実際に ReLU + 線形変換 の組み合わせでシグモイド関数を近似してみる。
重み $w$ とバイアス $b$ に具体的な値を入れて、隠れ層のノード数4の、2層のニューラルネットワークで近似すると次のようになる。

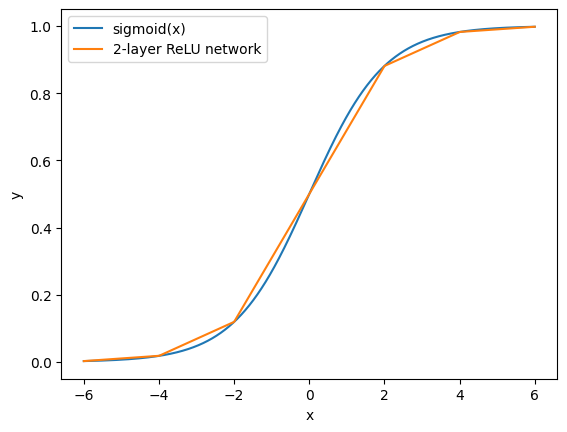
非線形のReLU関数を複数組み合わせることで、直線を折れ線状につなぎ合わせたような形で関数を近似していることが分かる。

シグモイド関数を近似したグラフは、数式で表すと次の形になる。これは、先ほど示した式に具体的な重み $w$ とバイアス $b$ の値を代入したものである。

$h_1=\mathrm{ReLU}(x+4)$
$h_2=\mathrm{ReLU}(x+2)$
$h_3=\mathrm{ReLU}(x−2)$
$h_4=\mathrm{ReLU}(x−4)$
$y=\mathrm{ReLU}\bigl( 0.00776x +0.0429\,h_1 +0.1398\,h_2 -0.1398\,h_3 -0.0429\,h_4 +0.0490 \bigr)$

実際には、これらの重み $w$ やバイアス $b$ は、モデルの出力と正解データとの誤差を最小化するように何度も更新することで、最も誤差が小さくなる値を見つけていく。（この過程が学習と呼ばれる）

活性化関数との組み合わせにより、層数を深くすればするほど表現力が上がり、より複雑な関数も近似できるようになっていく。

（引用）MIT Introduction to Deep Learning | 6.S191
https://youtu.be/alfdI7S6wCY?si=6L_TrNIcbJ_zRiCO

Q. なぜReLUは負の値を0にするのか？

ReLU関数は入力が負のとき、出力を0にする活性化関数である。
負の値もそのまま使いたい場合は、Leaky ReLU関数を使うという方法もある。これは負の領域に小さな傾きを持たせる。

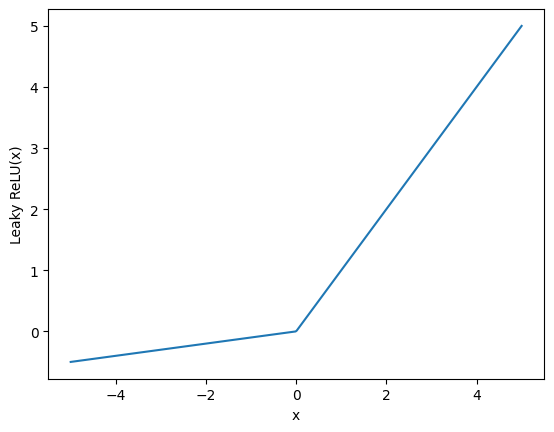
Leaky ReLU関数を使うことで、負の値が含まれることで勾配が完全に0になり、学習に二度と寄与しなくなってしまう「Dead ReLU」問題を防げる。
ただし、実際の学習では負の値を切り捨てても大きな問題にならないことが多い。あと個人的な感想として、最近の深層学習分野はReLUかGeLUが一般的で、Leaky ReLUはあまり使われてないように見える。

これは調べても決定的な理由っぽいものは載ってなかったものの、以下のRedditは参考になった。

What are the advantages of ReLU over the LeakyReLU (in FFNN)? - Reddit
https://www.reddit.com/r/MachineLearning/comments/4znzvo/what_are_the_advantages_of_relu_over_the/

負の値を0に切り捨てるReLUが使われている主な理由の一つは、出力が0になることでスパース性が生まれることが挙げられる。スパース性が高いと、重要な特徴だけが残りやすくなり、計算コストを抑えられる。また、小さな負の値はノイズになりやすく、学習を不安定にしてしまうことがあるため、不要な特徴による影響も遮断できる。

他にも、Leaky ReLUはハイパーパラメータとして負の傾き α を決める必要があり、チューニングが大変になる実装上の理由もありそう。